Pour atteindre les deux (petites) pages qu’occupe son article de Subsidia Pataphysica, Queneau a ajouté un texte en latin, sans traduction, dans lequel Jacob Bernoulli définit en 1691 la spirale logarithmique (sous le nom de spira mirabilis). J’avoue que je trouve assez cuistre de citer du latin sans traduction. Je précise donc que spira mirabilis veut dire « spirale miraculeuse » (ou merveilleuse), et j’ajoute que la dernière phrase de cette citation, eadem mutata resurgo, signifie « déplacée, je renais identique » (changée en moi-même).

Cette propriété d’invariance de cette spirale, qui avait frappé Bernoulli, n’est certainement pas satisfaite, ni par les spirales dessinées par Tavera ni par les gidouilles qui ornent les pages du journal. Ne me demandez pas ce que veulent dire les autres phrases de la citation, je ne parle pas le latin.

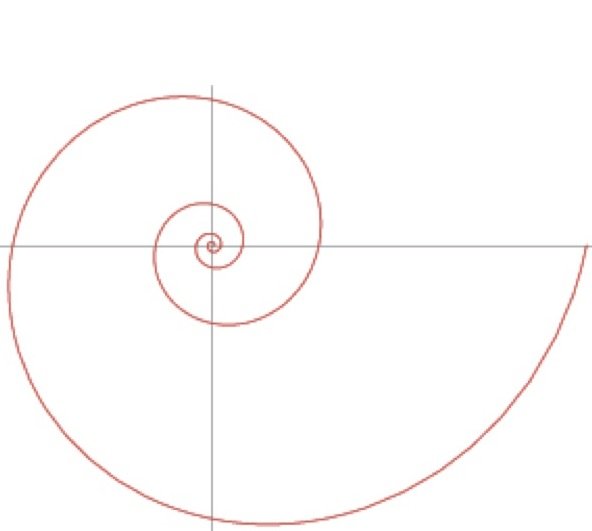
La spirale miraculeuse est une spirale logarithmique, la gidouille et la spirale de Tavera sont des spirales d’Archimède.

La différence est facile à comprendre : tracez une demi-droite à partir du centre de la spirale. Elle rencontre la spirale en une infinité de points. Dans la gidouille ou dans la spirale de Tavera, comme nous l’avons dit, ces points sont à égale distance les uns des autres. Ce n’est pas le cas dans la spirale logarithmique où les distances entre ces points augmentent exponentiellement (précisément, c’est pourquoi la spirale est dite « logarithmique ») lorsqu’on s’éloigne du centre. Par contre, l’angle que fait la spirale avec la demi-droite est le même en tous ces points. Ce qui n’est pas le cas pour la spirale d’Archimède.

Queneau ne le savait peut-être pas. En tout cas il n’y a pas de citation en grec ancien dans son article.

et ce n’est pas fini
suite à droite
$\to$