(avec Laura Monk et Guillaume Matheron)
1-1 / 2-2 / 3-3 / 4-3 / 5-5 / 6-6 / 7-4 / 8-4 / 9-9 / 10-6 / 11-11 / 12-10 / 13-9 / 14-14 / 15-5 / 16-5 / 17-12 / 18-18 / 19-12 / 20-10 / 21-7 / 22-12 / 23-23 / 24-21 / 25-8 / 26-26 / 27-20 / 28-9 / 29-29 / 30-30 / 31-6 / 32-6 / 33-33 / 34-22 / 35-35 / 36-9 / 37-20 / 38-30 / 39-39 / 40-27 / 41-41 / 42-8 / 43-28 / 44-11 / 45-12 / 46-10 / 47-36 / 48-24 / 49-15 / 50-50 / 51-51 / 52-12 / 53-53 / 54-18 / 55-36 / 56-14 / 57-44 / 58-12 / 59-24 / 60-55 / 61-20 / 62-50 / 63-7 / 64-7 / 65-65 / 66-18 / 67-36 / 68-34 / 69-69 / 70-46 / 71-60 / 72-14 / 73-42 / 74-74 / 75-15 / 76-24 / 77-20 / 78-26 / 79-52 / 80-33 / 81-81 / 82-20 / 83-83 / 84-78 / 85-9 / 86-86 / 87-60 / 88-29 / 89-89 / 90-90 / 91-60 / 92-18 / 93-40 / 94-18 / 95-95 / 96-48 / 97-12 / 98-98 / 99-99 / 100-33
(a-b signifie : la permutation spirale sur a éléments est d’ordre b. Dire que a=b, c’est dire que a est un nombre de Queneau.)
La suite (jusqu’à 1000) se trouve dans le fichier pdf obtenu en cliquant ici.
Et jusqu’à 10 000, dans le fichier xls obtenu en cliquant ici.
Le graphique ci-dessous représente lui aussi les ordres de ces permutations.
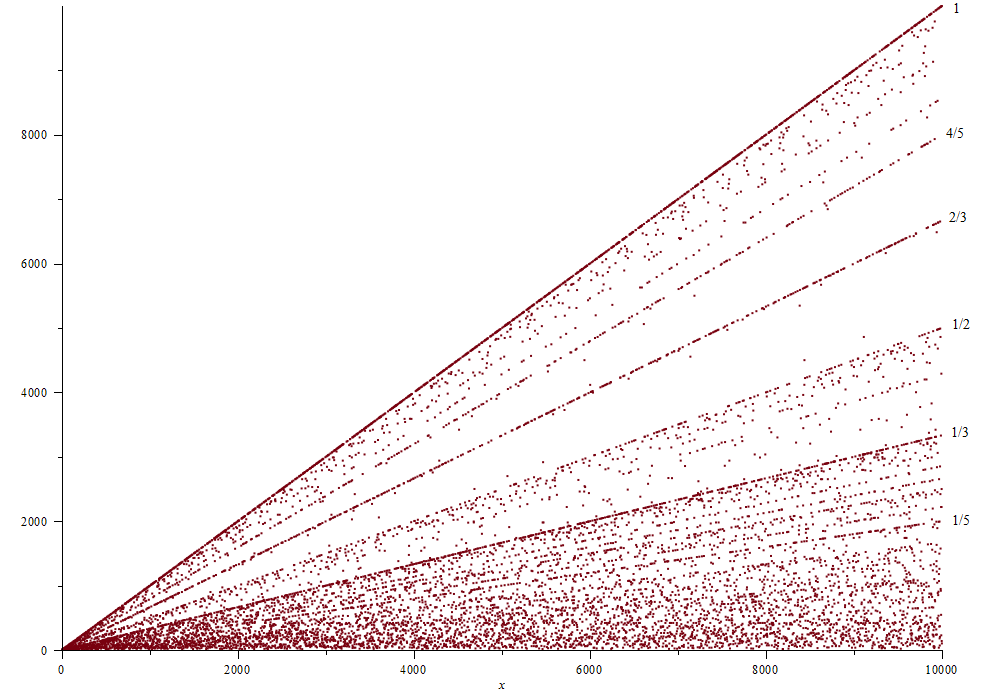
Enfin, voici les décompositions en cycles des « petites » permutations spirales (pour les nombres non de Queneau). L’écriture n = a + b + c … signifie que, pour la permutation spirale de n éléments, on trouve un groupe de a éléments permutés entre eux, un autre de b éléments, et ainsi de suite.
4=3+1 / 7=4+2+1 / 8=4+4 / 10=6+3+1 / 12=10+2 / 13=9+3+1 / 15=5+5+5 / 16=5+5+5+1 / 17=12+3+2 /
19=12+6+1 / 20=10+10 / 21=7+7+7 / 22=12+4+3+2+1 / 24=21+3 / 25=8+8+4+4+1 / 27=20+5+2 / 28=9+9+9+1 / 31=6+6+6+6+3+3+1 / 32=6+6+6+6+6+2 / 34=22+11+1 / 36=9+9+9+9 / 37=20+10+4+2+1 / 38=30+5+3 / 40=27+9+3+1 / 42=8+8+8+8+4+4+2 / 43=28+14+1 / 44=11+11+11+11 / 45=12+12+12+6+3
47=36+9+2
57=44+11+2
72=14+14+14+14+14+2
92=18+18+18+18+18+2