L’échange d’autographes de Gauss entre les deux messieurs avait eu lieu sans doute bien avant l’affaire Vrain-Lucas, puisque du vivant de Gauss, avant 1855 donc. Il n’est pas question de relater ici les détails de cette affaire. Voici l’essentiel : Chasles collectionnait les autographes, Chasles aimait les autographes, quelqu’un vint, un dénommé Vrain-Lucas, qui lui vendit ce qu’il désirait. Chasles aimait aussi l’Académie des sciences et décida de lui offrir le plus beau de ses autographes, une improbable lettre de Pascal, à croire laquelle lui, Pascal, aurait découvert la gravitation universelle (alors que Newton était âgé de onze ans) – une maladresse, déclenchant une querelle internationale qui ne grandit ni Chasles ni la confrérie. La notoriété de Michel Chasles, géomètre supérieur, était fort grande à l’étranger – en ce temps-là, le monde des mathématiciens était peu étendu. Par exemple, son Aperçu historique sur l’origine et le développement des méthodes en Géométrie, particulièrement de celles qui se rapportent à la géométrie moderne, publié à Bruxelles en 1837, fut traduit en allemand par Ludwig Adolf Sohnke sous le titre nettement plus fruste de Geschichte der Geometrie hauptsächlich mit Bezug auf die neueren Methoden, et cette traduction fut publiée à Halle dès 1839. Un autre exemple particulièrement ironique de sa notoriété est le fait qu’il a été le premier membre étranger de la London Mathematical Society. On a certainement noté que le point de contact de l’affaire des faux autographes et le Traité des coniques est Pascal, à qui le titre du Traité est d’ailleurs emprunté.
Tant a été écrit sur cette affaire. Mentionnons un livre Une Fabrique de faux autographes en 1870, un roman, l’Immortel, d’Alphonse Daudet, en 1888, dont le héros, qui ressemble assez peu à Chasles, finit par se jeter dans la Seine depuis le pont des Arts, encore un livre Le Parfait secrétaire des grands hommes en 1924, un article Michel Chasles « empereur de la géométrie » dupé par un faussaire par un académicien dans le Figaro du 4 juillet 1929, le Collectionneur ingénu toujours en 1929, Quetelet, Chasles et les faux Vrain-Lucas au Congrès national des sciences à Bruxelles en juin 1935 (Adolphe Quetelet fut, avec Germinal Pierre Dandelin, l’auteur d’une description dite « belge » des propriétés métriques des coniques (cette phrase pourrait engendrer de nombreuses digressions mais nous nous contentons de la figure ci-dessus) et c’est lui qui rendit compte de « l’affaire » à l’Académie belge), mention de l’Affaire par Marc Bloch dans son Apologie pour l’histoire en 1941, un autre article en marge de l’affaire Chasles dans le Flambeau en 1955, encore un article dans Isis, en 1968-69, les Relations de Chasles une émission de télévision le 24 octobre 1976, des articles Faux papiers dans Télérama le 14 octobre 1992, Escroc ès langues dans le Figaro, le 26 mai 1993, l’Affaire Chasles/Vrain-Lucas, en 2000 dans la revue d’histoire populaire Gavroche, un petit livre Mystification à l’Académie des sciences en 2001, Vrain-Lucas, le Balzac du faux dans la revue de la BNF en 2003, un article dans le Monde le 13 juillet 2005, un dans Découverte, la revue du Palais de la Découverte, en avril 2006…
 Ceci depuis 1870. Pendant le déroulement de l’affaire elle-même, il faut citer Défense de B. Pascal et accessoirement de Newton, Galilée, Montesquieu, etc., contre les faux documents présentés par M. Chasles à l’Académie des sciences, un livre de Prosper Faugère, un honnête spécialiste de Pascal, qui avait bien essayé de convaincre Michel Chasles personnellement, puis de convaincre Michel Chasles à l’Académie des sciences, que ses autographes de Pascal étaient des faux. Lui-même avait publié les Pensées et des lettres en 1844, il connaissait bien l’écriture manuscrite de Blaise Pascal, mais Chasles ne voulait rien entendre. L’Académie avait été divisée. Élie de Beaumont, qui avait argumenté d’un
Ceci depuis 1870. Pendant le déroulement de l’affaire elle-même, il faut citer Défense de B. Pascal et accessoirement de Newton, Galilée, Montesquieu, etc., contre les faux documents présentés par M. Chasles à l’Académie des sciences, un livre de Prosper Faugère, un honnête spécialiste de Pascal, qui avait bien essayé de convaincre Michel Chasles personnellement, puis de convaincre Michel Chasles à l’Académie des sciences, que ses autographes de Pascal étaient des faux. Lui-même avait publié les Pensées et des lettres en 1844, il connaissait bien l’écriture manuscrite de Blaise Pascal, mais Chasles ne voulait rien entendre. L’Académie avait été divisée. Élie de Beaumont, qui avait argumenté d’un
était « pour » Chasles, Balard aussi. Étaient contre Chasles, Le Verrier, très agressivement, Chevreul plus amicalement. Alors Faugère s’était résolu à livrer ce livre à la publicité. La plus intéressante observation est aujourd’hui dans le post-scriptum de sa préface, post-scriptum ajouté alors que l’impression du livre était presque terminée (la préface elle-même est datée du 1er juin 1868) et dont voici un extrait significatif :le style des grands hommes ne se contrefait pas,
Réapparition surprise de Thiers dans cette histoire – de ce grand politique, il nous restait à apprendre qu’outre avoir été un historien, il était aussi compétent en physique, il est vrai que pour un tel esprit, imaginer un lien entre pression et gravitation… Ah ! que la Commune n’a-t-elle pas poursuivi son travail d’élévation de la culture scientifique des masses !J’ai appris que l’un des membres les plus considérables de l’Institut, appartenant à la fois à l’Académie française et à celles des sciences morales et politiques, s’était notoirement prononcé pour la thèse soutenue par M. Chasles et qu’il admettait comme authentiques les écrits attribués à Pascal. L’illustre historien du Consulat et de l’Empire, que j’ai le profond regret de voir prêter l’autorité de son nom à une cause qui ne devait pas compter sur un tel honneur, a bien voulu m’expliquer sa manière de voir. Comme j’ai cru comprendre qu’il désirait se réserver l’occasion de publier lui-même les considérations sur lesquelles il fonde son opinion, je crois devoir m’abstenir de les révéler ici. Il me suffira de dire qu’elles se rattachent aux travaux de Pascal sur la pesanteur de la masse de l’air. Par une conséquence ingénieusement déduite de cet ordre de faits, M. Thiers arrive à cette conclusion, que Pascal a pu être naturellement amené jusqu’au seuil de la grande découverte de l’attraction sidérale ; et son intuition divinatrice aurait fait le reste.
et accéder à la suivante
cliquer sur le début de son titre
qui apparaît à doite de l’écran
Couverture : la première page de
Défense de B. Pascal et accessoirement de Newton, Galilée, Montesquieu, etc.,
de Prosper Faugère
(sur Gallica)
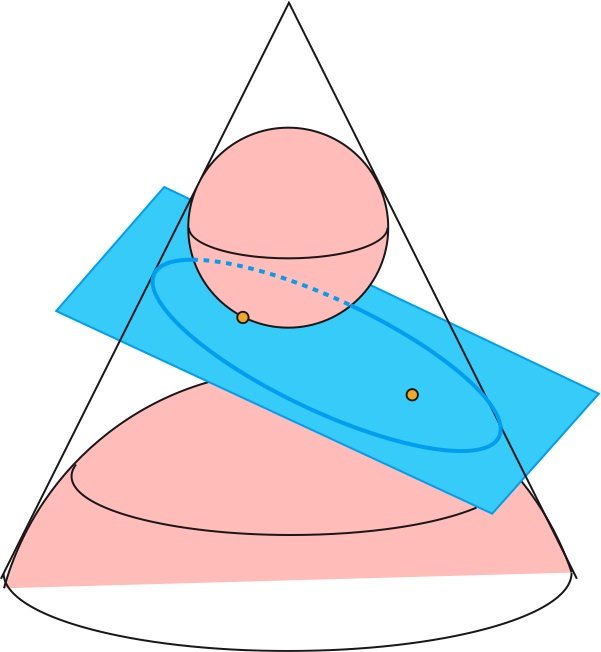
figure : les deux sphères tangentes au plan et au cône
déterminent les deux foyers de la conique
(un théorème belge), MA
le portrait de Michel Chasles
dans la sextine de l’introduction
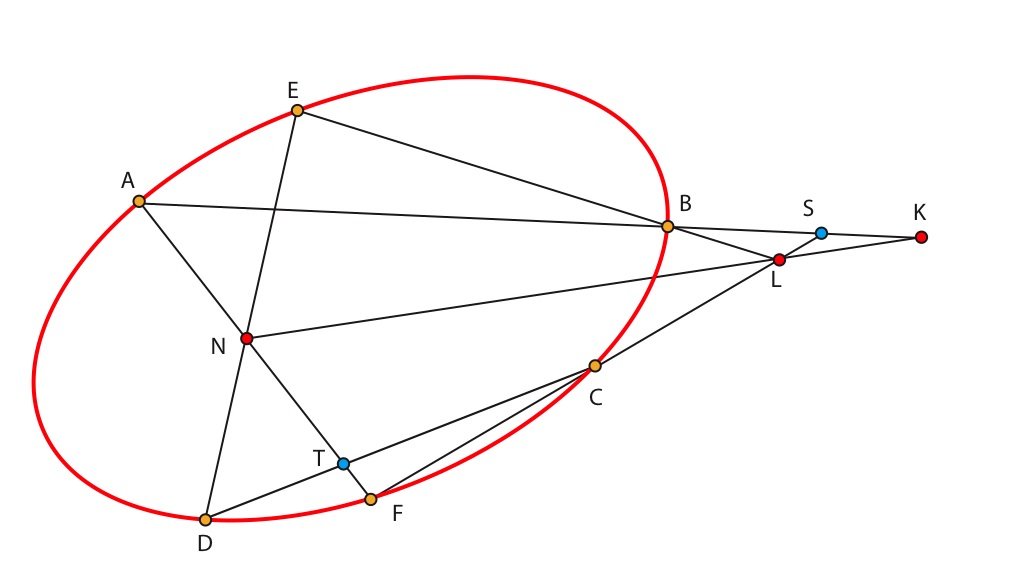
Soit K = (L N) $\cap$ (A B).