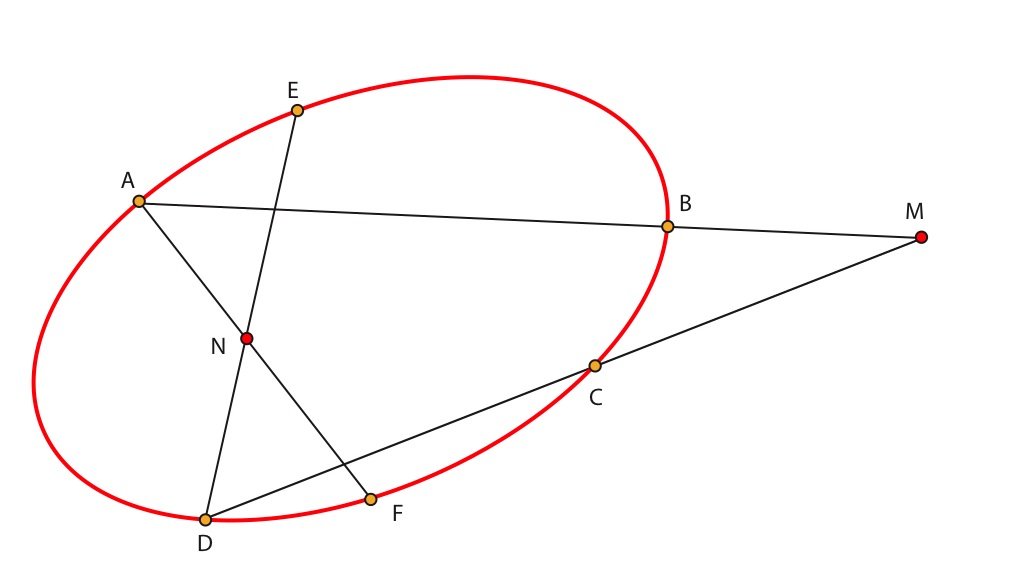
Quel est le nombre des normales qu’on peut abaisser d’un point sur une courbe d’ordre m et de classe n ?

Narratrice mathématicienne et préoccupée de l’élévation du niveau culturel et scientifique de ses lecteurs, je ne peux m’empêcher de leur signaler, de vous signaler, que ce nombre ne dépend que de m et qu’il est égal à m², ce qui n’est pas difficile à démontrer et n’occupe que le tout début de la note de Chasles en question, et qui indique que le journaliste avait dû avoir un exemplaire de ce texte entre les mains.
Quant à son texte à lui, son article dans l’Officiel, signalons que Louise Michel l’a lu, qui écrivit :

À l’Académie des sciences, les savants discutaient en paix, sans s’occuper de la Commune qui ne pesait pas sur eux.
Thénard, les Becquerel père et fils, Élie de Beaumont, se réunissaient comme de coutume.
À la séance du 3 avril, par exemple, M. Sédillot envoya une brochure sur le pansement des blessures sur le champ de bataille, le docteur Drouet sur les divers traitements du choléra, ce qui était tout à fait d’actualité, tandis que M. Simon Newcombe, un Américain, s’éloignait tout à fait du théâtre des événements et même de la terre en analysant au tableau le mouvement de la lune autour de la terre.
M. Delaunay, lui, rectifiait des erreurs d’observation météorologique sans s’occuper d’autre chose.

Thénard et les Becquerel sortent tout droit de l’article d’Hector Georges publié par l’Officiel le 24 mars. L’exemple n’était pas des mieux choisis puisque les Becquerel ont été assez peu présents pendant la Commune, Antoine Becquerel, qui avait 83 ans, n’assista qu’à la séance du 20 mars, son fils Edmond, lui, émargea les 13 et 20 mars. Ni l’un ni l’autre n’était présent ce 3 avril. L’encore plus jeune Henri Becquerel, qui devint plus tard le physicien le plus célèbre de la famille, découvrant la relativité avec Marie et Pierre Curie, n’avait alors que dix-neuf ans, n’en parlons pas.

L’Académie avait reçu, une fois de plus, une démonstration du théorème de Fermat, dont elle décida qu’elle serait transmise à Hermite. Ce dont chacun peut déduire que Charles Hermite n’était pas présent. Et en effet, pas plus qu’Hervé Faye, Charles Hermite n’a signé la liste d’émargement du 3 avril. Joseph Bertrand n’était pas là non plus.

À quatre heures et demie, l’huissier ferma la porte du côté de l’antichambre. La réunion du comité secret lut et adopta le procès-verbal de la réunion précédente, l’ordre du jour appelait la reprise de la discussion de la proposition d’Henri Sainte-Claire Deville, mais on se contenta d’enregistrer le fait que les textes des motions de Dumas et Combes, selon lesquels rien ne devait être modifié, avaient bien été autographiés et distribués, Chevreul fit quelques observations, il semble que Sainte-Claire Deville, qui était présent ce jour-là comme nous avons déjà pu le constater, ne se soit pas exprimé (mais peut-être avait-il quitté la grande salle plus tôt, par la petite salle et l’escalier en colimaçon), quant à Dumas et Combes, ils n’étaient là ni l’un ni l’autre. On leva la séance, qui n’avait duré cette fois que quinze minutes, ce qui fait que l’on peut imaginer, on imagine beaucoup dans ce chapitre, qu’il y eut peu de bavardages. Le comité secret suivant n’eut lieu qu’après la fin de ce récit, le 26 juin, et s’occupa d’organiser le remplacement du mathématicien Gabriel Lamé, qui était mort depuis le 1^er mai 1870, plus d’un an auparavant.

La démonstration de la propriété « qui sert de base à toute la théorie de ces courbes »:

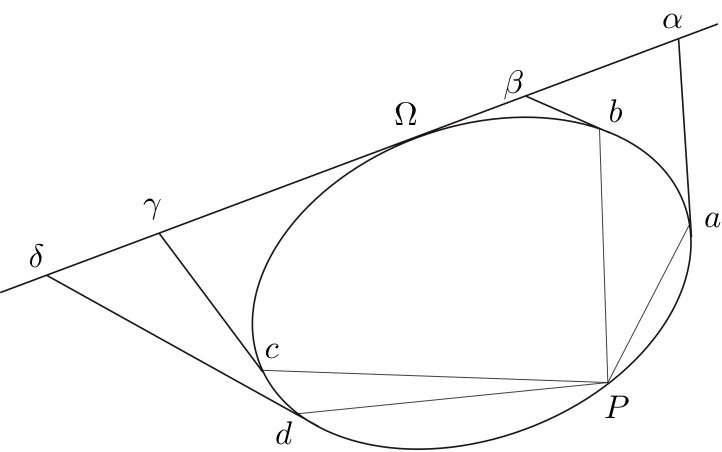
Si par quatre points d’une conique on mène les tangentes et quatre autres droites aboutissant à un cinquième point quelconque de la courbe, le rapport anharmonique de ces quatre droites sera égal à celui des quatre points de rencontre des quatre tangentes et d’une cinquième tangente quelconque.

– au tout début du Traité des coniques de Michel Chasles, se conclut par un :

Donc, etc.
 

pour « tourner la page »
et accéder à la suivante
cliquer sur le début de son titre
qui apparaît à doite de l’écran

Couverture : les Comptes rendus
du 3 avril 1871
figure : décrite dans le texte, MA
 

La figure du 3 avril :


M = (A B) $\cap$ (C D),