Il faudrait les présenter, au moins en présenter quelques-uns. Choisissons six membres de la confrérie, six de ceux qui participèrent aux séances de ce mois de mars.
(a) Charles Hermite, pour commencer, car une telle personnalité mérite d’occuper la première place, un mathématicien, conservateur et clérical, bourgeois, oui, mais la plupart des académiciens étaient des bourgeois, et c’était le cas de tous les mathématiciens, il faudra attendre encore, attendre les effets de la troisième République, pour qu’un fils d’ouvrier, comme Henri Lebesgue en 1922 ou un fils de forgeron, comme Élie Cartan en 1931, vienne s’asseoir dans un fauteuil vert, un homme de pouvoir, oui, mais être membre de l’Académie des sciences était une position de prestige et de pouvoir. Charles Hermite, donc. Quarante-neuf ans en 1871 et qui avait passé la période du siège à Bordeaux avec l’École polytechnique était repliée et où il avait donné son cours, du 2 janvier au 6 février. Les photographies lui donnent un air revêche, qu’il fût imbu de son importance ou tout simplement tourmenté, le mot « bourru » ne paraît pas lui convenir. Charles Hermite a entretenu une correspondance abondante avec plusieurs collègues en France ou à l’étranger, et cette correspondance constitue aujourd’hui une inépuisable source d’informations. La guerre qui venait de s’achever a durablement marqué ce Lorrain. Un de ses titres de gloire, la démonstration de la transcendance de $e$, le fameux nombre
$$e=1+\frac{1}{1}+\frac{1}{2}+\frac{1}{6}+\frac{1}{24}+\cdots=\sum_{n=0}^\infty\frac{1}{n !}=2{,}718\ldots$$
ne satisfait à aucune relation
$$\sum_{k=0}^ma_ke^k=0$$
pour des $a_k$ entiers, était à venir. Il publia cette démonstration deux ans plus tard, à l’âge de 51 ans, remarquons ici que l’idée qu’un mathématicien ne peut être productif qu’avant quarante ans est d’invention récente.
Nommons les cinq autres par ordre alphabétique.
(b) Joseph Bertrand, ensuite, sur le pouvoir duquel il y aurait beaucoup à écrire, tant du côté de ses liens familiaux avec le pouvoir financier, un euphémisme pour désigner le grand capital, par exemple avec la famille de banquiers Péreire, que du côté du pouvoir académique. Il était membre de l’Institut, puisqu’il se trouvait, en mars 1871, dans l’ovale (à vrai dire rectangulaire) que forment les fauteuils verts, mais sa plus grande période de pouvoir « académique » était encore à venir, non pas parce qu’il avait encore un théorème remarquable à démontrer, mais parce qu’il fut, trois ans après la fin de cette histoire, élu secrétaire perpétuel, perpétuel c’est-à-dire jusqu’à sa mort (il était pourtant aussi « immortel », au sens de « membre de l’Académie française ») en 1900. Des théorèmes remarquables, il ne semble pas que, lui qui avait été un élève brillant et précoce, auditeur à l’École polytechnique à l’âge de 11 ans et reçu premier dans cette école à 17 ans, il en ait démontré beaucoup. Il est vrai que, auprès de la transcendance de $e$, l’étude de la série numérique
$$\sum_{n=2}^{+\infty}\dfrac{1}{n^\alpha(\log n)^\beta},$$
(dont il montra qu’elle était convergente si et seulement si $\alpha$>1 ou $\alpha$=1 et $\beta$>1, un exercice modérément intéressant pour étudiants de deuxième année), fait piètre figure. À vrai dire, il existe aussi des « courbes de Bertrand » et d’autres travaux de Joseph Bertrand, de sorte que le réduire aux « séries de Bertrand » est une légère injustice. Signalons sans attendre qu’il y aura de pires injustices dans ce texte…
(c) Et puis Michel Chasles qui, si ceci était un roman, un roman banal avec un héros, serait ce héros. De Michel Chasles on disait beaucoup de choses. Qu’il avait entretenu une liaison avec une danseuse de l’Opéra, bien longtemps auparavant, mais qu’il vivait depuis en célibataire, qu’il ne buvait jamais de vin, qu’il avait été agent de change avant de devenir un géomètre supérieur, un titre qu’il méritait sans aucun doute puisque l’on avait créé pour lui une « chaire de géométrie supérieure » à la Sorbonne. Oui, on disait pas mal de choses à son sujet. Un homme âgé déjà, soixante-dix-huit ans, aimable, doux, paisible, indulgent, en particulier avec les élèves qu’il interrogeait pour le baccalauréat, naïf et confiant comme un enfant, un homme enfin à qui l’Académie des sciences servait de famille.
(d) Charles Delaunay, un fils de géomètre (ici le mot géomètre désigne un autre métier que dans le paragraphe précédent…) devenu professeur de géométrie puis astronome, l’air bon enfant sur les photographies, avec son visage large dont on disait qu’il ressemblait à la Lune, par imitation ajoutait-on. Car le mouvement de la lune était sa spécialité. Cinquante-cinq ans. Charles Delaunay avait maintenu l’activité de service public de l’Observatoire pendant le siège, les relevés météorologiques en particulier, Charles Delaunay continua à maintenir l’activité scientifique de l’Observatoire dans les circonstances difficiles créées par le second siège de Paris et la guerre civile qui s’annonçaient.
(e) Léonce Élie de Beaumont, comme les précédents un ancien polytechnicien, un géologue, théoricien des montagnes et auteur de la première carte géologique de la France. Il était secrétaire perpétuel de l’Académie des sciences, un des deux secrétaires perpétuels, ce qu’il resta jusqu’à sa mort en 1874. Il fut remplacé, on l’a sans doute compris, par Joseph Bertrand. Soixante-douze ans, peut-être déjà fatigué, nous verrons en tout cas que sa voix était assez faible. Son épouse, qui avait tenu salon et qui écrivait des poèmes (et qu’il convient de ne pas confondre avec Madame Leprince de Beaumont, qui, elle, écrivait des contes), était morte depuis quatre ans.
(f) Hervé Faye enfin. Cinquante-sept ans, professeur à l’École polytechnique et astronome lui aussi, dont une comète, qu’il avait découverte en 1843, porte le nom et continue à suivre sa trajectoire, conique comme l’exigent les lois de Kepler, et plus précisément dans ce cas elliptique, et à réapparaître tous les sept ans et demi. Hervé Faye fut un des premiers astronomes à utiliser la photographie, au cours de l’éclipse de soleil de 1858. Il était vice-président de l’Académie des sciences, faisant office de président, le président était empêché, ainsi Faye avait-il présidé toutes les séances depuis janvier.
La figure du 20 mars :
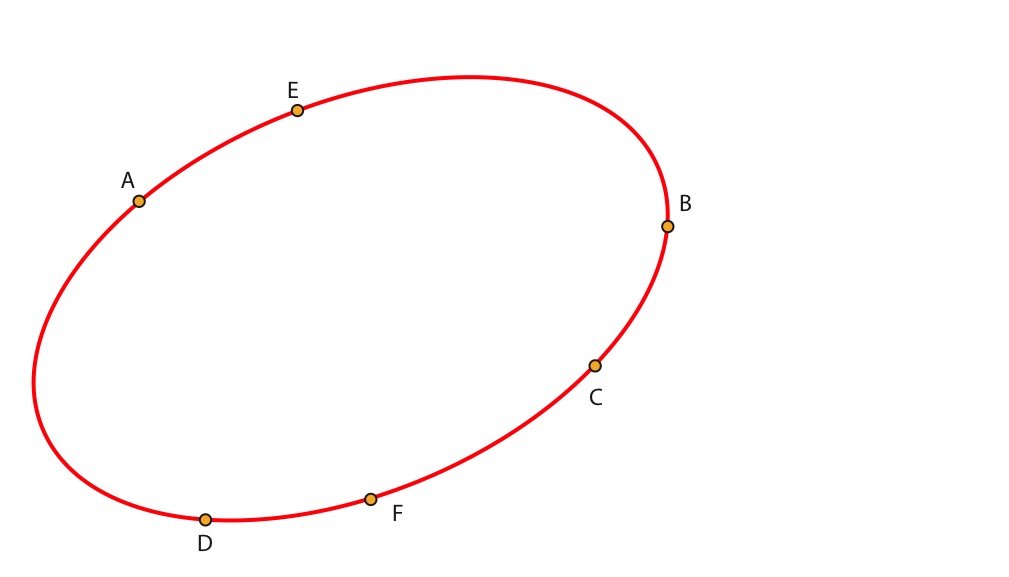
… et soient A, B, C, D, E, F six points sur cette conique.
Cette suite de récits a été organisée grâce à une suite de figures (une pour chaque lundi) illustrant un théorème de géométrie, le « théorème de Pascal ». La figure du 13 mars était très simple, tout simplement une ellipse, ce cercle un peu aplati, qui symbolise ici la salle des séances de l’Académie des sciences. Des points vont apparaître sur cette figure en même temps que de nouveaux personnages entreront dans le récit.
Sur l’ellipse, les six points A, B, C, D et E sont les six académiciens présentés dans les chapitres « 20 mars ».
(a) Charles Hermite, pour commencer, car une telle personnalité mérite d’occuper la première place, un mathématicien, conservateur et clérical, bourgeois, oui, mais la plupart des académiciens étaient des bourgeois, et c’était le cas de tous les mathématiciens, il faudra attendre encore, attendre les effets de la troisième République, pour qu’un fils d’ouvrier, comme Henri Lebesgue en 1922 ou un fils de forgeron, comme Élie Cartan en 1931, vienne s’asseoir dans un fauteuil vert, un homme de pouvoir, oui, mais être membre de l’Académie des sciences était une position de prestige et de pouvoir. Charles Hermite, donc. Quarante-neuf ans en 1871 et qui avait passé la période du siège à Bordeaux avec l’École polytechnique était repliée et où il avait donné son cours, du 2 janvier au 6 février. Les photographies lui donnent un air revêche, qu’il fût imbu de son importance ou tout simplement tourmenté, le mot « bourru » ne paraît pas lui convenir. Charles Hermite a entretenu une correspondance abondante avec plusieurs collègues en France ou à l’étranger, et cette correspondance constitue aujourd’hui une inépuisable source d’informations. La guerre qui venait de s’achever a durablement marqué ce Lorrain. Un de ses titres de gloire, la démonstration de la transcendance de $e$, le fameux nombre
$$e=1+\frac{1}{1}+\frac{1}{2}+\frac{1}{6}+\frac{1}{24}+\cdots=\sum_{n=0}^\infty\frac{1}{n !}=2{,}718\ldots$$
ne satisfait à aucune relation
$$\sum_{k=0}^ma_ke^k=0$$
pour des $a_k$ entiers, était à venir. Il publia cette démonstration deux ans plus tard, à l’âge de 51 ans, remarquons ici que l’idée qu’un mathématicien ne peut être productif qu’avant quarante ans est d’invention récente.
Nommons les cinq autres par ordre alphabétique.
(b) Joseph Bertrand, ensuite, sur le pouvoir duquel il y aurait beaucoup à écrire, tant du côté de ses liens familiaux avec le pouvoir financier, un euphémisme pour désigner le grand capital, par exemple avec la famille de banquiers Péreire, que du côté du pouvoir académique. Il était membre de l’Institut, puisqu’il se trouvait, en mars 1871, dans l’ovale (à vrai dire rectangulaire) que forment les fauteuils verts, mais sa plus grande période de pouvoir « académique » était encore à venir, non pas parce qu’il avait encore un théorème remarquable à démontrer, mais parce qu’il fut, trois ans après la fin de cette histoire, élu secrétaire perpétuel, perpétuel c’est-à-dire jusqu’à sa mort (il était pourtant aussi « immortel », au sens de « membre de l’Académie française ») en 1900. Des théorèmes remarquables, il ne semble pas que, lui qui avait été un élève brillant et précoce, auditeur à l’École polytechnique à l’âge de 11 ans et reçu premier dans cette école à 17 ans, il en ait démontré beaucoup. Il est vrai que, auprès de la transcendance de $e$, l’étude de la série numérique
$$\sum_{n=2}^{+\infty}\dfrac{1}{n^\alpha(\log n)^\beta},$$
(dont il montra qu’elle était convergente si et seulement si $\alpha$>1 ou $\alpha$=1 et $\beta$>1, un exercice modérément intéressant pour étudiants de deuxième année), fait piètre figure. À vrai dire, il existe aussi des « courbes de Bertrand » et d’autres travaux de Joseph Bertrand, de sorte que le réduire aux « séries de Bertrand » est une légère injustice. Signalons sans attendre qu’il y aura de pires injustices dans ce texte…
(c) Et puis Michel Chasles qui, si ceci était un roman, un roman banal avec un héros, serait ce héros. De Michel Chasles on disait beaucoup de choses. Qu’il avait entretenu une liaison avec une danseuse de l’Opéra, bien longtemps auparavant, mais qu’il vivait depuis en célibataire, qu’il ne buvait jamais de vin, qu’il avait été agent de change avant de devenir un géomètre supérieur, un titre qu’il méritait sans aucun doute puisque l’on avait créé pour lui une « chaire de géométrie supérieure » à la Sorbonne. Oui, on disait pas mal de choses à son sujet. Un homme âgé déjà, soixante-dix-huit ans, aimable, doux, paisible, indulgent, en particulier avec les élèves qu’il interrogeait pour le baccalauréat, naïf et confiant comme un enfant, un homme enfin à qui l’Académie des sciences servait de famille.
(d) Charles Delaunay, un fils de géomètre (ici le mot géomètre désigne un autre métier que dans le paragraphe précédent…) devenu professeur de géométrie puis astronome, l’air bon enfant sur les photographies, avec son visage large dont on disait qu’il ressemblait à la Lune, par imitation ajoutait-on. Car le mouvement de la lune était sa spécialité. Cinquante-cinq ans. Charles Delaunay avait maintenu l’activité de service public de l’Observatoire pendant le siège, les relevés météorologiques en particulier, Charles Delaunay continua à maintenir l’activité scientifique de l’Observatoire dans les circonstances difficiles créées par le second siège de Paris et la guerre civile qui s’annonçaient.(e) Léonce Élie de Beaumont, comme les précédents un ancien polytechnicien, un géologue, théoricien des montagnes et auteur de la première carte géologique de la France. Il était secrétaire perpétuel de l’Académie des sciences, un des deux secrétaires perpétuels, ce qu’il resta jusqu’à sa mort en 1874. Il fut remplacé, on l’a sans doute compris, par Joseph Bertrand. Soixante-douze ans, peut-être déjà fatigué, nous verrons en tout cas que sa voix était assez faible. Son épouse, qui avait tenu salon et qui écrivait des poèmes (et qu’il convient de ne pas confondre avec Madame Leprince de Beaumont, qui, elle, écrivait des contes), était morte depuis quatre ans.
(f) Hervé Faye enfin. Cinquante-sept ans, professeur à l’École polytechnique et astronome lui aussi, dont une comète, qu’il avait découverte en 1843, porte le nom et continue à suivre sa trajectoire, conique comme l’exigent les lois de Kepler, et plus précisément dans ce cas elliptique, et à réapparaître tous les sept ans et demi. Hervé Faye fut un des premiers astronomes à utiliser la photographie, au cours de l’éclipse de soleil de 1858. Il était vice-président de l’Académie des sciences, faisant office de président, le président était empêché, ainsi Faye avait-il présidé toutes les séances depuis janvier.
pour « tourner la page »
et accéder à la suivante
cliquer sur le début de son titre
qui apparaît à doite de l’écran
Couverture : la liste des membres de l’Académie des sciences,
Comptes rendus, volume 72 (1871)
portrait de Charles Delaunay, extrait de la sextine
de l’introduction
et accéder à la suivante
cliquer sur le début de son titre
qui apparaît à doite de l’écran
Couverture : la liste des membres de l’Académie des sciences,
Comptes rendus, volume 72 (1871)
portrait de Charles Delaunay, extrait de la sextine
de l’introduction
La figure du 20 mars :
… et soient A, B, C, D, E, F six points sur cette conique.
Cette suite de récits a été organisée grâce à une suite de figures (une pour chaque lundi) illustrant un théorème de géométrie, le « théorème de Pascal ». La figure du 13 mars était très simple, tout simplement une ellipse, ce cercle un peu aplati, qui symbolise ici la salle des séances de l’Académie des sciences. Des points vont apparaître sur cette figure en même temps que de nouveaux personnages entreront dans le récit.
Sur l’ellipse, les six points A, B, C, D et E sont les six académiciens présentés dans les chapitres « 20 mars ».