J’ai trouvé une quantité extraordinaire de propriétés et de théorèmes. Je me suis intéressé à la géométrie du triangle depuis pratiquement le collège. C’est dû à deux causes : j’ai une mentalité à m’intéresser à ce genre de choses d’abord, ensuite, c’est une chose facile. Tout est facile en mathématiques à un certain niveau et tout devient difficile. C’est pourquoi il y avait tellement de fabricants de théorèmes du triangle, c’est que ce n’était pas difficile. Un peu comme en théorie des nombres. Et en géométrie du triangle, il peut se produire les mêmes difficultés qu’en théorie des nombres.
Je m’intéressais surtout aux céviennes dans le triangle – pas uniquement, bien sûr. J’avais noté dans un cahier une très grande quantité de résultats, pas très intéressants. Je me suis amusé à calculer par exemple les hauteurs en fonction des bissectrices, les bissectrices en fonction des médianes, etc., mais il y avait un point sur lequel je m’étais penché et qui n’a pas attiré l’attention d’autres mathématiciens, c’est ce qu’on pourrait appeler les céviennes hétérogènes concourentes. C’est-à-dire : dans un triangle, est-il possible qu’une hauteur, la hauteur du côté A, la bissectrice du côté B et la médiane du côté C concourent ? C’est le genre d’idée biscornue qui m’est assez propre et qui devient tout de suite terriblement difficile.
J. M. L. L. Ce n’est vrai que pour les triangles particuliers.
Marie-Adèle : vous voulez boire quelque chose ?
F. L. L. Exactement. Autrement dit, j’aurais voulu définir de tels triangles, c’est-à-dire quels sont les angles A,B,C, ou quels sont les côtés par rapport aux autres côtés, etc. J’y ai repensé de nouveau, d’une part à Fresnes et d’autre part à Dora, mais à Dora, ma pensée était trop relâchée pour pouvoir penser à quelque chose de compliqué. On peut montrer comment un tel triangle serait possible : tu te donnes un segment de droite, avec deux extrémités A et B et tu te donnes une direction et la hauteur : tu as dans ce cas la bissectrice, la hauteur, tu n’as qu’à joindre le milieu, ça te donne le troisième sommet. (un croquis s’impose)
__________________
Les “céviennes” (du nom du mathématicien (italien, XVIIIe siècle) Ceva, ou plus exactement de son théorème) sont des droites issues des sommets d’un triangle.
On dit que ce sont des céviennes si elles sont concourantes. Par exemple, les trois hauteurs sont concourantes, les médianes aussi et tout autant les bissectrices. MA
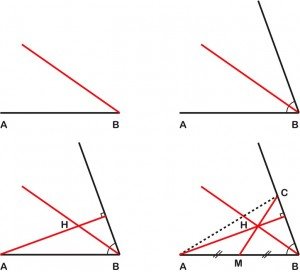
Ce que propose FLL est le disparate absolu : construire un triangle dont une hauteur, une bissectrice et une médiane soient concourantes. La figure montre la construction telle que décrite par FLL : 1. le segment AB et la bissectrice en B (rouge), 2. le mêmes avec la droite noire qui sera BC, 3. la hauteur issue de A (rouge), qui rencontre la bissectrice en H, 4. la droite (rouge) joignant le milieu M de BC à H, qui, puisque ces trois « céviennes disparates » sont concourantes, est la médiane et détermine le point C. MA