F. L. L. Non, pas tellement. Mais j’ai pu constater qu’il y a un type d’activité dont je suis de moins en moins capable – non pas que ça ait cessé de m’intéresser – c’est une création mathématique ou échiquéenne intense. C’est elle qui m’a quitté. Maintenant, je ne peux plus rien faire de vraiment intense, on ne peut pas demander de faire l’amour à soixante-quinze ans comme à vingt, non plus des mathématiques ou des échecs.
J. H. Est-ce que vous maîtrisez le processus ? Comment ça s’est passé ? Est-ce au niveau de la mémoire, de la capacité d’abstraction, ou…?
F. L. L. Je ne commence à perdre la mémoire que depuis trois ou quatre ans. Vous ne pouvez pas vous en rendre compte, mais il y a quelque temps, je vous aurais donné beaucoup plus de choses. C’était un peu pathologique chez moi.
J. M. Vous êtes devenu normal !
F. L. L. Oui… j’ai tout de même des trous. D’une certaine manière, il n’est pas mauvais que j’aie oublié beaucoup de choses, parce que ma mémoire d’il y a seulement dix ans m’encombrerait pour ce livre. On a pu parler un peu de girafe ou de choses de cet ordre, j’en ai des millions comme ça, heureusement, j’en ai oublié. Mais je sais que les choses vraiment importantes, je ne les ai pas oubliées, les choses qui font ma personnalité, mes processus de conduite. C’est de mon érudition que tombent des tas de choses. Je n’en souffre pas beaucoup pour ce livre. Les choses qui tombent sont des choses délicieuses mais pas importantes. Je pourrais me souvenir avoir mangé un saint-honoré délicieux, mais voilà, je ne m’en souviens plus, et on n’a peut-être pas besoin de l’imprimer. Mais je n’ai rien perdu de ma mémoire des choses fondamentales. Tolstoï a des souvenirs de l’époque où il était au sein, moi pas. Ma mémoire remonte à peu près à ma troisième année, et encore, des petits souvenirs épars, pas une mémoire continue. Jusqu’à maintenant, j’ai l’impression de quelque chose qui n’a pas changé en moi, alors que beaucoup de choses ont changé. J’ai été enfant, un vrai enfant ; jeune, un vrai jeune ; adulte, un vrai adulte et maintenant je suis un vieux croulant et j’ai encore quelque temps devant moi. J’ai donc changé en capacité d’intelligence, de mémoire, physique, sexuelle, visuelle, auditive, etc., mais je sens très bien qu’il y a quelque chose qui ne change pas, je me sens le même, d’une certaine façon difficile à définir, qu’à douze ans. Je le sens très bien. C’est quelque chose qui n’a pas changé et qui n’est pas desservi par ma perte de mémoire – perte épisodique. Pour l’intelligence, c’est la même chose. Donc, j’ai gardé l’essentiel.
Mes capacités intellectuelles ont été en augmentant. Je les avais développées. J’étais certainement un enfant précoce – je ne dis pas surdoué – dans la capacité de comprendre des choses du domaine du raisonnement.
Il y a une quinzaine d’années, j’ai été invité par l’association des anciens élèves du collège de Melun. Le président, un homme du même âge que moi, un vieil avocat qui doit voter entre Lecanuet et Giscard, un brave type, m’a présenté et a raconté quelques anecdotes sur moi avant de me laisser en raconter d’autres. Il a raconté que quand j’étais en classe de seconde – il était en troisième – j’avais institué un commerce illicite : je vendais, contre des bouchées au chocolat, les dissertations de première et de philo et les problèmes de math et de physique. Intellectuellement, j’étais certainement en avance, je faisais les problèmes de math et de physique de première et de philo alors que j’étais en seconde. Je le faisais très bien.
(retrouver le document témoin, sinon, ne pas garder cette histoire)
J’ai eu très vite des capacités intellectuelles développées, capacités de création que l’on trouve chez les mathématiciens et les joueurs d’échecs ; je suis justement à l’intersection des deux. Vers trente-cinq ans, je n’avais plus cette capacité. Cela ne veut pas dire qu’on devient rien du tout à ce moment-là; on peut avoir de bonnes idées – il y a des cas de longévité plus grande – et puis on peut comprendre très loin. En dehors de cela, mes capacités dans le domaine de l’observation n’ont jamais été ni en avance ni en retard, je savais assez bien observer, mais plutôt 9/20 que 1½0. J’avais de l’avance dans l’intelligence/abstraction, dans la mémoire et dans la sensibilité. Voilà mes trois domaines.
J. M. Dans le cas des échecs et des mathématiques, qu’est-ce qui vous a lâché ? C’est la capacité de concentration ?
F. L. L. Oui, uniquement. L’intérêt ne m’a jamais manqué, mais de plus en plus l’intérêt de connaître les travaux des autres. En mathématiques, je ne me sentais plus capable de rien faire, alors que quand j’étais jeune, je faisais des créations – qui n’avaient pas grande valeur, je le sais bien – mais qui étaient des créations. Quand j’avais environ dix-huit ans, j’ai créé un chapitre des mathématiques qui sera oublié de l’humanité. J’étais parti d’une idée d’ailleurs très fausse, je m’en suis rendu compte plus tard. Voilà l’idée :
Qu’est-ce que c’est que la multiplication ? Ce n’est jamais qu’une addition de choses identiques. Qu’est-ce que c’est que la puissance ? a puissance a (aa), c’est a x a x a etc. Pourquoi ne pas continuer, m’étais-je dit, et j’ai créé une opération que j’ai appelée l’émergence : a => b.
a => b, c’est aa, le tout puissance a : (aa)a, le tout puisssance a, etc.. J’ai étudié les propriétés de l’émergence et de ce que j’ai appelé l’extrence ; soustraction, division, extraction de racines, etc.. J’ai trouvé tout un tas de théorèmes là-dessus, qui n’ont pas un grand intérêt.
J. M. Il n’y a pas de structure de groupe là-dessus, c’est pour ça que c’est faible.
F. L. L. Exactement. Ces théorèmes sont vrais, sont justes, et sans intérêt. D’ailleurs, quand je faisais ça, je ne savais pas ce qu’était un groupe.
J. M. Vous ne l’auriez pas fait.
F. L. L. Exactement. J’ai découvert que j’avais un prédécesseur : Leibniz. Il s’est intéressé à x [x puissance x (MA)], c’est-à-dire à x 2 [x=>2 (idem)]. Il a cherché d’abord la dérivée, c’est beaucoup plus difficile de dériver x [x puissance x (idem)] que beaucoup d’autres fonctions plus élémentaires. Une fois de plus, je me trouvais dans la mentalité de Leibniz. Je pense que lui aussi devait se poser des problèmes de ce genre, et lui non plus n’a eu le sentiment du groupe – Oui, il l’a eu au niveau des nombres entiers, bien sûr.
Donc, ce genre de travaux avaient peu de valeur, c’est certain, mais c’était de la création. J’en ai fait aussi à l’époque où la géométrie du triangle était bien vue – maintenant, naturellement, c’est la fin de tout – et j’avais trouvé je ne sais plus quels théorèmes qui auraient certainement honoré une publication de prof de math vers 1860. J’en avais des tas de nouveaux. D’ailleurs maintenant, en dehors des maths modernes, il y a un courant pour revenir à de belles choses de ce genre. Un très joli bouquin vient de paraître qui parle justement… qui va au-delà de l’hexagramme mystique de Pascal. Je continue à lire avec plaisir ce que les autres ont fait, ça m’intéresse moins de les trouver.
Donc perte des capacités créatrices un peu intenses, au niveau de l’abstraction.
J. M. Est-ce que vous pensez que l’affaiblissement de votre intérêt est la conséquence de la perte des capacités créatrices ou que c’en serait, éventuellement, une cause ?
F. L. L. Bien sûr, c’est une question que je me suis posée, mais je ne connais pas la réponse. Il est certain qu’en vieillissant, on se désabuse un peu, on perd de l’intérêt pour certaines choses…
J. M. Perte de motivation plutôt que d’intérêt. On peut garder son intérêt mais être moins motivé.
F. L. L. Oui, c’est sûr… Je crois quand même que la baisse de mes facultés a précédé la perte de mes motivations. Je crois qu’on peut avoir envie de faire l’amour, même quand on ne peut plus. Mais je reste toujours passionné pour beaucoup de choses, j’ai un peu moins de motivations. C’est le problème des relectures. Il y a des textes qui m’ont enthousiasmé, je vous ai parlé d’un poème sur un flocon de neige, par exemple, qui est pour moi une chose merveilleuse ; finalement, je ne sais pas si j’ai envie de le relire, j’ai peur de ne pas y retrouver un plaisir aussi vif.
Voilà ce que je peux appeler le bon emploi de mon temps, et qui me fait dire que j’ai vécu 10% de plus que la plupart des autres.
__________________
La notation de FLL pour ce que nous avons noté ici “a=>b” utilisait la double flèche comme ici mais disposée verticalement. Il élève a à la puissance a, puis recommence cette opération un certain nombre de fois, b est le nombre de a qu’il faudrait écrire dans la formule.
Par exemple, (a=>1)=a, (a=>2)=a puissance a, etc.
JMLL fait remarquer que ce n’est pas un groupe. C’est simplement parce que (a=>b)=>c n’est pas toujours égal à a=>(b=>c). Ou encore plus simplement parce que 1=>b est toujours égal à 1.
FLL discute ensuite le cas de xx (x puissance x). Pour dériver cette fonction de x, on a besoin de logarithmes (et la dérivée en est (ln(x)+1) xx). MA
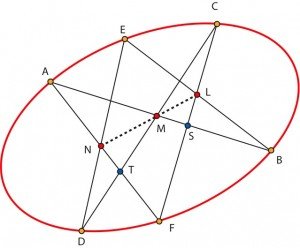
L’hexagramme mystique de Pascal est le nom du “théorème de Pascal”, déjà mentionné dans une note du chapitre 58,
que l’on voit illustré ici et qui dit que
- étant donnés six points sur une conique (une ellipse sur la figure),
- les diagonales de l’hexagone que forment ces six points se coupent en trois points (les points L, M et N)
- qui sont alignés.
MA