Les grandes vacances précédant le 3 octobre 1908, au mois de juillet, je n’avais pas sept ans, je me trouvais bien tranquille à l’ombre dans une pièce. Il faisait très chaud, beaucoup de gens faisaient la sieste. J’ai pris un de mes protège-cahiers, au dos desquels étaient imprimées des tables de multiplication. C’était une table des multiples de 1, de 2, jusqu’aux multiples de 9. J’avais déjà remarqué – sans doute pas très longtemps auparavant – certaines particularités, que j’exprime de manière plus abstraite et plus lucide, évidemment Les multiples d’un nombre pair sont toujours des nombres pairs ; les multiples des nombres impairs sont tantôt pairs, tantôt impairs. Dans les multiples de 9, il y a beaucoup de curiosités : le multiple de 9 par un nombre de 1 chiffre est formé de 1 ou 2 chiffres dont la somme fait toujours 9 – je retrouvais les éléments de la preuve par 9. J’avais donc apprécié cette propriété des nombres entiers.
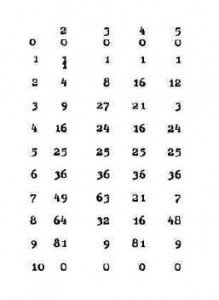
Je reviens à ce chaud après-midi de juillet. J’eus l’idée d’écrire les nombres entiers les uns après les autres – je me souviens très bien les avoir écrits horizontalement, c’est plus naturel, mais quelques jours plus tard, je reprenais la même chose dans l’ordre vertical : 1 2 3 4 5 6 7 8 9 10.
Bien des années après, je me suis rendu compte qu’on pouvait mettre 0, mais je ne pensais pas du tout à 0 à six ans trois quarts. Puis, j’ai écrit en-dessous les carrés des nombres, j’ai multiplié les nombres par eux-mêmes, je ne connaissais pas le mot “carré”: 1 4 9 16 25 36 49 64 8l 100. J’ai regardé cela et tout à coup, j’ai eu une illumination. Je me suis rendu compte qu’il y avait une chose très intéressante, à condition qu’on ne tienne pas compte des dizaines. J’en ai été un peu choqué, pourquoi ne pas en tenir compte ! Mais c’est un fait : en ne regardant que le chiffre des unités, je me suis aperçu que, le 5 étant au milieu, à égale distance du 5, c’est le même chiffre : 6 et 6, 9 et 9, 4 et 4, 1 et 1 – rajoutons 0 et 0.
J’ai été ébloui, absolument ébloui. Ce n’est pas une très grande propriété mathématique, mais j’étais jeune et je l’avais trouvée moi-même, c’est une possibilité de créativité qui [était] une chose très importante.. C’est là que j’ai senti, que ma vie se fixait, toute ma vie, tout entière, jusqu’à ma mort, jusqu’après la publication de ce livre – et, en effet, c’est bien cela. Puis, je me suis dit : Si on multiplie comme cela, si je fais ce que j’appelle maintenant les cubes, les quatrièmes puissances, cinquièmes…, ça sera forcément intéressant ! C’était intéressant ici, ça ne va pas devenir un désordre, un chaos, quelque chose manquant d’intérêt. Par conséquent, je n’ai qu’à faire une colonne de plus et je trouverai quelque chose d’intéressant puis encore une colonne après, et comme je savais que la suite des nombres entiers est illimitée, je n’aurai qu’à continuer toute ma vie. Quand j’aurai un moment de libre, je prendrai à la dernière colonne où je me suis arrêté et je ferai la colonne suivante. Je tomberai forcément sur des merveilles, sur des harmonies, sur des choses curieuses. En attendant, je vais en faire quelques unes jusqu’au dîner. Je vais faire les cubes (encore une fois, je n’appelais pas encore cela : “cube”.), et je n’ai gardé que les unités : 1 8 7 4 5 6 3 2 9 0.
J .M. A ce moment-là déjà vous avez fait le raisonnement avec seulement les unités ?
F. L. L. Ah, pour les cubes, oui.
J. M. A l’âge de sept ans, c’est un signe de maturité et de raisonnement mathématique.
F. L. L. J’avais le sentiment qu’il n’y avait que les unités qui comptaient, et en même temps le sentiment bizarre que quelque chose ne tournait pas rond dans les mathématiques, les dizaines, les centaines, etc. J’ai regardé la ligne des cubes, j’ai cherché et je n’ai pas trouvé. J’ai insisté, excluant la possibilité qu’il n’y ait rien d’intéressant, j’étais sur une pente certaine. Je cherchais par rapport au 5, mais ça n’est pas symétrique par rapport au 5. Mais, en répétant ces deux nombres qui sont à égale distance du 5, qui ne sont pas les mêmes, en les répétant, ça a surgi tout à coup : la somme des chiffres à égale distance de part et d’autre du 5 est la même ( 4 et 6, 3 et 7, 2 et 8, 9 et 1, 0 et 0) Autrement dit, j’avais de la symétrie dans la colonne des carrés, dans la colonne des cubes, j’avais de la complémentarité. J’étais donc encore tombé sur quelque chose de très beau, et différent.
Comme j’avais encore pas mal de temps avant le dîner, je me suis dit : “Je vais faire ce que j’appelle maintenant les 4ème puissances : 1 6 1 6 5 6 1 6 1 0.” Je me souviens très bien avoir pensé – et c’est normal – que ça allait être encore plus difficile pour les quatrièmes puissances : “En passant des carrés aux cubes, j’ai eu du mal à trouver. Je vais avoir encore plus de mal, tant mieux !” Il y a une symétrie comme dans les carrés, mais en plus, il y a répétition par glissement : 1 6, 1 6 puis 6 1, 6 1.
J. M. Est-ce que vous avez, à cette période, réalisé qu’une puissance quatrième était un carré, donc, que forcément la symétrie devait se retrouver ?
F. L. L. Je ne crois pas, je ne crois pas. Pour ça, il a fallu attendre un peu plus longtemps, évidemment.
J’avais encore du temps avant le dîner pour la cinquième puissance ; ça me donnait : 1 2 3 4 5 6 7 8 9 0 . On retrouve exactement les chiffres des premières puissances. Je découvrais la loi que la cinquième puissance d’un nombre entier se termine par la même unité que ce nombre entier. C’était quelque chose de très étonnant et de très merveilleux de voir se reconstituer exactement la même chose, mais en même temps, c’était un gouffre qui s’ouvrait, une tragédie, parce que ma vie était terminée. Ma vie était terminée parce que je savais que la sixième puissance serait comme la seconde, la septième comme la troisième, par conséquent que je n’avais plus rien à trouver. J’ai eu l’impression d’avoir terminé les mathématiques ce que j’appelais le calcul. Donc, un effet étonnant, effrayant, que je ne saurais pas très bien définir, que j’ai même oublié.
Mais je suis sûr d’avoir subi cet effet-là d’une manière très forte. Je suis donc allé dîner et me coucher, sachant que ce n’était pas la peine de recommencer le lendemain. Et puis, je ne pouvais quand même pas me résigner et le lendemain, j’ai repris cette chose-là, j’ai bien regardé et je me suis demandé si je ne pouvais pas encore trouver quelque chose. Je ne me résignais pas à voir ma vie arrêtée à cet endroit-là. Et je me suis rendu compte que le 5 se répète tout le temps ; le 6 se répète aussi, dans toutes les puissances ; et puis le 1.
Je me suis rendu compte que le 5 se répète tout le temps, dans toutes les puissances ; le 6 aussi, et puis le 1 – je rajoute le 0, je n’y avais pas pensé à ce moment-là. Par contre, il y a des nombres qui ne se répètent pas à chaque fois : le nombre 2 ne se répète qu’à la cinquième, et le nombre 3, le nombre 7 aussi et le nombre 8 aussi. Et puis, il y a le cas intermédiaire : c’est le 4, qui se répète au milieu, et le 9 qui se répète au milieu. J’avais trois sortes de nombres, et c’était déjà intéressant de les classer. Après avoir constaté que ces nombres ne se comportaient pas de la même manière, je me suis rendu compte que si [à] un nombre d’une classe on ajoute 5, on reste toujours dans la classe :
Là, je me suis rendu compte que, finalement, les mathématiques n’étaient probablement pas terminées. Il y avait de l’espoir, mais à condition de ne pas avoir toujours la même manière de voir les choses, de changer sa manière d’appréhender les nombres – pour moi, les mathématiques, c’était les nombres uniquement à cette époque-là. Ensuite, j’ai compris que je pouvais faire autre chose et j’ai continué. Je me suis rendu compte que je trouvais toujours quelque chose d’intéressant dans l’arithmétique – ce que j’appelais le calcul. La géométrie, c’est venu beaucoup plus tard.
__________________
Les grandes vacances précédant le 3 octobre 1908, au mois de juillet,
La suprenante précision de cette datation tient au fait que le 3 octobre est le jour de l’anniversaire de François Le Lionnais. [AFG]

Comments