Ce qui est facile à mesurer, sur le terrain ou sur la mer, ce sont les angles. Pourtant, sur un plan, sur une carte, les angles sont sujets à caution. Voici pourquoi. La somme des angles d’un triangle dessiné sur un plan vaut 180°. Or la somme des angles d’un triangle dessiné sur une sphère (ou sur la Terre, même si celle-ci n’est pas exactement sphérique) est toujours plus grande que 180°. 

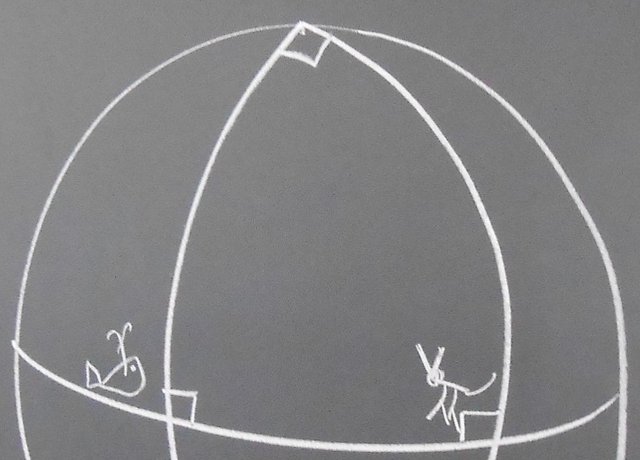Par exemple, le triangle formé par un ours polaire, une baleine au large du delta de l’Amazone et une gazelle au Kenya a trois angles droits.

Ceci a pas mal de conséquences (plus ou moins graves) pour les cartographes et les utilisateurs de cartes. Aucune de ces conséquences n’est perceptible sur le plan d’une ville : la différence entre la somme des angles d’un triangle et 180° est d’autant plus petite que le triangle est plus petit et un plan de ville ne couvre qu’une infime partie de la Terre.

9 avril 2014
(à suivre)

$\Rightarrow$  base, cercle, conforme, géoïde